Keltischer Knoten: Unterschied zwischen den Versionen
Anna (Diskussion | Beiträge) |
Anna (Diskussion | Beiträge) (→YouTube Channel) |
||
| (35 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
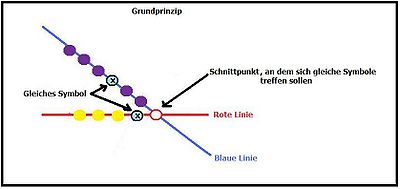
| − | + | = Das Grundprinzip dieser Rätselart<br> = | |
| − | + | {| cellspacing="1" cellpadding="1" style="width: 877px; height: 1438px;" | |
| − | + | ||
| − | {| cellspacing="1" cellpadding | + | |
|- | |- | ||
| valign="top" | | | valign="top" | | ||
| Zeile 18: | Zeile 16: | ||
<span style="font-size: smaller;">(In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand <span style="color: rgb(255, 0, 0);">O</span>)</span> | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand <span style="color: rgb(255, 0, 0);">O</span>)</span> | ||
| − | Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen. | + | Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen.<br> |
| − | + | | valign="top" align="center" | [[Datei:Keltischer-knoten-grundprinzip.jpg|400px]] | |
| − | + | ||
| − | | [[ | + | |
|- | |- | ||
| valign="top" | | | valign="top" | | ||
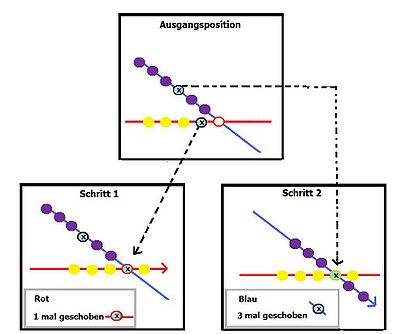
Beispiel: | Beispiel: | ||
| − | Wir haben eine rote und eine blaue Strecke, auf der unterschiedliche Symbole angeordnet sind. Wobei es im Beispiel unerheblich ist, welche Symbole sich hinter den lila oder gelben Punkten verbergen. Konzentrieren wir uns auf die Symbole, die mit einem '''<span style="background-color: rgb(204, 255, 255);">X</span>''' gekennzeichnet sind und sich sowohl auf der roten als auf der blauen Linie (Strecke) befinden. | + | Wir haben eine <span style="color: rgb(255, 0, 0);"><span style="background-color: rgb(255, 255, 255);">rote </span></span>und eine <span style="color: rgb(0, 0, 128);"><span style="background-color: rgb(255, 255, 255);">blaue </span></span>Strecke, auf der unterschiedliche Symbole angeordnet sind. Wobei es im Beispiel unerheblich ist, welche Symbole sich hinter den lila oder gelben Punkten verbergen. Konzentrieren wir uns auf die Symbole, die mit einem '''<span style="background-color: rgb(204, 255, 255);">X</span>''' gekennzeichnet sind und sich sowohl auf der <span style="color: rgb(255, 0, 0);">roten </span>als auf der <span style="color: rgb(0, 0, 128);">blauen </span>Linie (Strecke) befinden. |
Stellen wir uns diese Strecken nun als Fließbänder vor, die bewegt werden können. | Stellen wir uns diese Strecken nun als Fließbänder vor, die bewegt werden können. | ||
| − | <span style="font-size: smaller;">(Schritt 1) </span> | + | <span style="font-size: smaller;">(Schritt 1) </span> |
| − | Um das '''<span style="background-color: rgb(204, 255, 255);">X</span> '''gekenntzeichnete Symbol auf der roten Strecke zum Schnittpunkt <span style="color: rgb(255, 0, 0);">O </span>der beiden Strecken zu bringen, muß die rote Strecke einmal nach rechts verschoben werden. | + | Um das '''<span style="background-color: rgb(204, 255, 255);">X</span> '''gekenntzeichnete Symbol auf der <span style="color: rgb(255, 0, 0);">roten </span>Strecke zum Schnittpunkt <span style="color: rgb(255, 0, 0);">O </span>der beiden Strecken zu bringen, muß die <span style="color: rgb(255, 0, 0);">rote </span>Strecke einmal nach rechts verschoben werden.<span style="font-size: smaller;"> |
| − | + | </span> | |
| − | <span style="font-size: smaller;"> | + | |
<span style="font-size: smaller;">(Schritt 2) </span> | <span style="font-size: smaller;">(Schritt 2) </span> | ||
| − | Jetzt muß die blaue Strecke bewegt werden, um das mit '''<span style="background-color: rgb(204, 255, 255);">X</span>''' gekennzeichnete Symbol ebenfalls zum Schnittpunkt <span style="color: rgb(255, 0, 0);">O </span>zu bewegen. Drei-maliges Verschieben der blauen Strecke in Pfeilrichtung bringt uns zur Lösung.< | + | Jetzt muß die <span style="color: rgb(51, 51, 153);">blaue </span>Strecke bewegt werden, um das mit '''<span style="background-color: rgb(204, 255, 255);">X</span>''' gekennzeichnete Symbol ebenfalls zum Schnittpunkt <span style="color: rgb(255, 0, 0);">O </span>zu bewegen. Drei-maliges Verschieben der <span style="color: rgb(0, 0, 128);">blauen </span>Strecke in Pfeilrichtung bringt uns zur Lösung.<span style="font-size: smaller;"> |
| + | </span> | ||
| − | <span style="font-size: smaller;"> | + | <span style="font-size: smaller;"><span style="font-size: larger;">Die Reihenfolge, in der die Strecken verschoben werden, ist unerheblich. Man hätte im Beispiel auch zuerst mit der blauen Strecke beginnen können.</span></span><br> |
| − | + | | valign="top" | [[Datei:Keltischer-knoten-einführung.jpg|400px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | | [[ | + | |
|- | |- | ||
| valign="top" | | | valign="top" | | ||
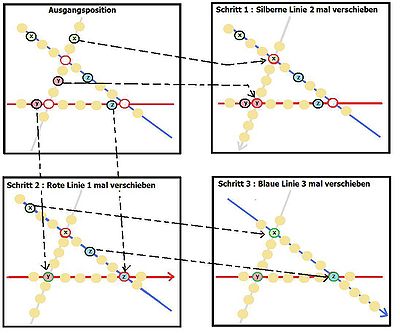
| − | In | + | In nächsten Beispiel: |
| − | + | haben wir 3 Strecken mit unterschiedlichen Symbolen und Schnittpunkten. | |
| − | + | Am Schnittpunkt <span style="color: rgb(128, 128, 128);"><u>silber </u></span><u>- </u><span style="color: rgb(0, 0, 128);"><u>blau</u> </span>können sich die <span style="background-color: rgb(204, 255, 204);">'''X'''</span> , | |
| − | am Schnittpunkt <u> | + | am Schnittpunkt <span style="color: rgb(128, 128, 128);"><u>silber </u></span><u>- </u><span style="color: rgb(255, 0, 0);"><u>rot</u> </span>die '''<span style="background-color: rgb(255, 153, 204);">Y</span>''' und |
| − | <span style=" | + | am Schnittpunkt <span style="color: rgb(0, 0, 128);"><u>blau </u></span><u>- </u><span style="color: rgb(255, 0, 0);"><u>rot</u> </span>die mit '''<span style="background-color: rgb(204, 255, 255);">Z</span>''' gekennzeichneten Symbole treffen. |
| − | <span style="font-size: smaller;"> | + | <span style="font-size: smaller;">(Schritt 1)</span> |
| − | + | <span style="font-size: smaller;"> </span>Beginnen wir mit der <span style="color: rgb(128, 128, 128);">silbernen </span>Strecke und verschieben sie um zwei Positionen in Pfeilrichtung. Sowohl das <span style="background-color: rgb(204, 255, 204);">'''X'''</span> als auch das '''<span style="background-color: rgb(255, 153, 204);">Y</span>''' befinden sich jetzt an den Schnittpunkten zu der <span style="color: rgb(0, 0, 128);">blauen </span>und <span style="color: rgb(255, 0, 0);">roten </span>Strecke. | |
<span style="font-size: smaller;">(Schritt 2) </span> | <span style="font-size: smaller;">(Schritt 2) </span> | ||
| − | Bewegen wir jetzt die rote Strecke um eine Postition in Pfeilrichtung, erkennen wir, daß die <span style="background-color: rgb(255, 153, 204);">'''Y'''</span> Symbole auf der Schnittstelle <u>silber- rot </u>übereinstimmen | + | Bewegen wir jetzt die <span style="color: rgb(255, 0, 0);">rote </span>Strecke um eine Postition in Pfeilrichtung, erkennen wir, daß die <span style="background-color: rgb(255, 153, 204);">'''Y'''</span> Symbole auf der Schnittstelle <span style="color: rgb(128, 128, 128);"><u>silber</u></span><u>- <span style="color: rgb(255, 0, 0);">rot</span> </u>übereinstimmen. Das <span style="background-color: rgb(204, 255, 255);">'''Z'''</span> Symbol der <span style="color: rgb(255, 0, 0);">roten </span>Strecke ist zwar schon auf der richtigen Position der Schnittstelle <span style="color: rgb(0, 0, 128);"><u>blau </u></span><u>- </u><span style="color: rgb(255, 0, 0);"><u>rot</u></span>, aber deckt sich noch nicht mit dem <span style="background-color: rgb(204, 255, 255);">'''Z'''</span> Symbol der <span style="color: rgb(0, 0, 128);">blauen </span>Strecke. |
<span style="font-size: smaller;">(Schritt 3)</span> | <span style="font-size: smaller;">(Schritt 3)</span> | ||
| − | Jetzt bewegen wir die blaue Strecke um 3 Positionen in Pfeilrichtung und erhalten sowohl auf der <u>silber - blauen</u> als auch auf der <u>blau - roten</u> Schnittstelle Übereinstimmungen mit den bereits dahinverschobenen Symbolen <span style="background-color: rgb(204, 255, 204);">'''X'''</span> und <span style="background-color: rgb(204, 255, 255);">'''Z'''</span> der anderen Strecken. | + | Jetzt bewegen wir die <span style="color: rgb(0, 0, 128);">blaue </span>Strecke um 3 Positionen in Pfeilrichtung und erhalten sowohl auf der <span style="color: rgb(128, 128, 128);"><u>silber </u></span><u>- </u><span style="color: rgb(0, 0, 128);"><u>blauen</u> </span>als auch auf der <span style="color: rgb(0, 0, 128);"><u>blau </u></span><u>- </u><span style="color: rgb(255, 0, 0);"><u>roten</u></span> Schnittstelle Übereinstimmungen mit den bereits dahinverschobenen Symbolen <span style="background-color: rgb(204, 255, 204);">'''X'''</span> und <span style="background-color: rgb(204, 255, 255);">'''Z'''</span> der anderen Strecken. <br> |
| − | | [[ | + | Die Aufgabe ist somit erfüllt. |
| + | |||
| + | | valign="top" | [[Datei:Keltischer-knoten-einführung1.jpg|400px]] | ||
| + | |} | ||
| + | |||
| + | = Formenbeispiele = | ||
| + | |||
| + | {| width="200" cellspacing="1" cellpadding="1" | ||
|- | |- | ||
| − | | | + | | [[Datei:Keltischer-knoten-kreis-6jpg.jpg|250px]] |
| − | | | + | | [[Datei:Keltischer-knoten-6.jpg|250px]] |
| + | | | ||
| + | [[Datei:Keltischer-knoten-10.jpg|250px]] | ||
| + | |||
|} | |} | ||
| − | + | Wie sich die Strecken bilden ist der Phantasie des Designers überlassen. Grundvoraussetzung für den Keltischen Knoten ist aber immer ein Flechtmuster und der Bandverlauf muss endlos sein, was bei den Runescaperätseln allerdings nicht gegeben ist. | |
| − | {| | + | Beispiel eines einfachen Keltischen Knotens [[Datei:Keltischer-knoten-einfache-ausführung.png|50px]] |
| + | |||
| + | Es gibt zahlreiche Möglichkeiten und hier werden nur einige Ideen aufgeführt, die nach dem Prinzip der Runescaperätsel dargestellt werden. Das Wichtigste für das Lösen dieser Rätsel sind die Schnittpunkte und die Vorstellungskraft, dass die Strecken wie ein Fließ- oder Förderband in beide Richtungen bewegt werden können, mit dem Ziel zwei gleiche Symbole auf die betreffende Schnittstelle zu bringen.<br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | = Die Keltischen Knoten von Runescape<br> = | ||
| + | |||
| + | {| width="200" cellspacing="1" cellpadding="1" | ||
|- | |- | ||
| − | + | | | |
| − | + | [[Datei:Keltischer-knoten6.png|400px]] | |
| + | |||
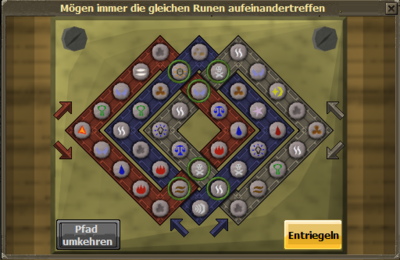
| + | Keltischer Knoten mit 6 übereinstimmenden Schnittpunkten<br> | ||
| + | |||
| + | | valign="top" | | ||
| + | [[Datei:Keltischer-knoten8.png|400px]] | ||
| + | |||
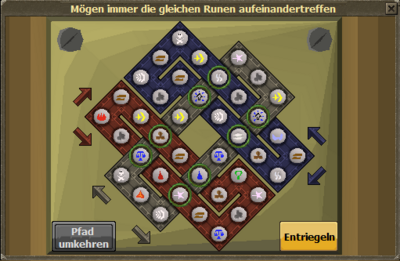
| + | Keltischer Knoten mit 8 übereinstimmenden Schnittpunkten<br> | ||
| + | |||
|- | |- | ||
| − | | <br> | + | | valign="top" | |
| − | | | + | [[Datei:Keltischer-knoten10.png|400px]] |
| + | |||
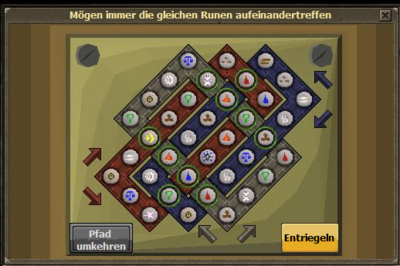
| + | Keltischer Knoten mit 10 übereinstimmenden Schnittpunkten<br> | ||
| + | |||
| + | | valign="top" | | ||
| + | [[Datei:Keltischer-knoten12.png|400px]] | ||
| + | |||
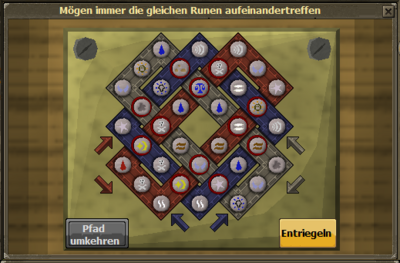
| + | Keltischer Knoten mit 12 übereinstimmenden Schnittpunkten<br> | ||
| + | |||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | = Lösung eines Keltischen Knotenrätsels = | ||
| + | |||
| + | {| width="922" cellspacing="1" cellpadding="1" style="" | ||
|- | |- | ||
| − | | | + | | valign="top" align="left" | |
| − | | align=" | + | [[Datei:Keltischer-knoten.png|400px]] |
| + | |||
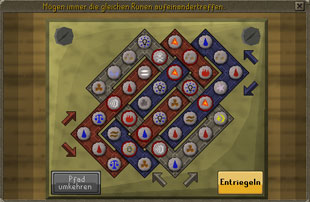
| + | Sofern sich keine zwei gleichen Runensymbole auf einem Schnittpunkt befinden, wird das Feld rot umrandet sein. Die Aufgabe ist jetzt, die jeweiligen Strecken so zu verschieben, dass gleiche Runen an den Schnittpunkten übereinander liegen.<br> | ||
| + | |||
| + | | valign="top" align="left" | | ||
| + | [[Datei:Keltischer-knoten10.png|400px]] | ||
| + | |||
| + | Erst wenn beide Runen auf einem Schnittpunkt gleich sind, erscheint eine grüne Umrandung, die euch anzeigt, dass ihr richtig verschoben habt. Als gelöst gilt das Rätsel, wenn alle Schnittpunke übereinstimmen.<br> | ||
| + | |||
|- | |- | ||
| − | | | + | | valign="top" align="left" colspan="2" | |
| − | + | <br> | |
| − | + | ||
| − | + | <br> Eine Lösungsidee ist es, sich eine markante und wenn möglich nur einmal vorhandene Rune auf der roten Strecke zu merken (um die Anzahl der Drehungen nachvollziehen zu können) und dann die blaue Strecke mit den entsprechenden Pfeilsymbolen im Uhrzeigersinn zu drehen, wobei auf die Schnittpunkte zu achten ist. | |
| − | + | ||
| − | + | Sollten sich während einer kompletten Drehung der blauen Strecke (16 mal - auch hier merkt man sich eine markante Rune) keine Übereinstimmung mit der roten Strecke ergeben (zu Erkennen an der grünen Umrandung der Schnittstellen) wird die rote Strecke um ein Symbol weiter gedreht und die blaue Strecke erneut im Uhrzeigersinn bis zu 16 mal verschoben. | |
| − | + | ||
| − | + | Dies muss gemacht werden, bis sich alle rot - blauen Schnittstellen decken, also grün umrandet sind. (Bei 10 Schnittstellen gibt es nur zwei mögliche zwischen rot und blau)<br> | |
| + | |||
| + | Ist das erreicht, wird die silberen Strecke gedreht, bis sich alle Schnittstellen decken. | ||
| + | |||
| + | Sollte es keine komplette Lösung geben, obwohl die Schnittstellen der blau - roten Strecken richtig waren, muss nach einer anderen Kombination zwischen blau und rot gesucht werden, um danach wieder die silberne Strecke zu bewegen.<br> | ||
| + | |||
| + | Die Reihenfolge der Verschiebung der Strecken ist auch hier unbedeutend, wobei es sich empfiehlt erst die Strecken mit den geringsten Schnittpunkten zu wählen. | ||
| + | |||
| + | Geübte Rätsellöser werden durch genaue Betrachtung des Bildes schon vorher einige Möglichkeiten ausschließen können und sich durch Kombinationsgabe schneller zum Ziel bewegen. | ||
| + | |||
| + | Allen anderen bleibt erstmal nur der Weg des mühsamen Verschiebens der Strecken, was aber auch zur Lösung verhelfen wird. | ||
| + | |||
| + | Viel Erfolg und schöne Belohnungen. | ||
| + | |||
|} | |} | ||
| − | [[Category:Schatzsuche]] | + | =YouTube Channel= |
| + | [[Datei:Pentzel - Logo rund.png|link=https://www.youtube.com/watch?v=4dEGfvS_pWw LetsPlay Pentzel Channel|Pentzel]] | ||
| + | |||
| + | [[Category:Schatzsuche Grundlagen]] | ||
| + | [[Kategorie:Schatzsuche - Gesamtübersicht]] | ||
Aktuelle Version vom 24. November 2018, 16:11 Uhr
Inhaltsverzeichnis
Das Grundprinzip dieser Rätselart
Formenbeispiele
|
|
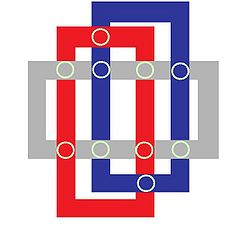
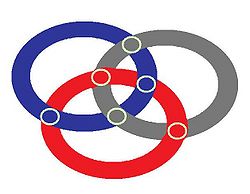
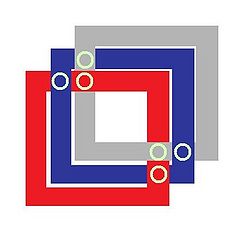
Wie sich die Strecken bilden ist der Phantasie des Designers überlassen. Grundvoraussetzung für den Keltischen Knoten ist aber immer ein Flechtmuster und der Bandverlauf muss endlos sein, was bei den Runescaperätseln allerdings nicht gegeben ist.
Beispiel eines einfachen Keltischen Knotens 
Es gibt zahlreiche Möglichkeiten und hier werden nur einige Ideen aufgeführt, die nach dem Prinzip der Runescaperätsel dargestellt werden. Das Wichtigste für das Lösen dieser Rätsel sind die Schnittpunkte und die Vorstellungskraft, dass die Strecken wie ein Fließ- oder Förderband in beide Richtungen bewegt werden können, mit dem Ziel zwei gleiche Symbole auf die betreffende Schnittstelle zu bringen.
Die Keltischen Knoten von Runescape
|
Keltischer Knoten mit 6 übereinstimmenden Schnittpunkten |
Keltischer Knoten mit 8 übereinstimmenden Schnittpunkten |
|
Keltischer Knoten mit 10 übereinstimmenden Schnittpunkten |
Keltischer Knoten mit 12 übereinstimmenden Schnittpunkten |
Lösung eines Keltischen Knotenrätsels
|
Sofern sich keine zwei gleichen Runensymbole auf einem Schnittpunkt befinden, wird das Feld rot umrandet sein. Die Aufgabe ist jetzt, die jeweiligen Strecken so zu verschieben, dass gleiche Runen an den Schnittpunkten übereinander liegen. |
Erst wenn beide Runen auf einem Schnittpunkt gleich sind, erscheint eine grüne Umrandung, die euch anzeigt, dass ihr richtig verschoben habt. Als gelöst gilt das Rätsel, wenn alle Schnittpunke übereinstimmen. |
|
Sollten sich während einer kompletten Drehung der blauen Strecke (16 mal - auch hier merkt man sich eine markante Rune) keine Übereinstimmung mit der roten Strecke ergeben (zu Erkennen an der grünen Umrandung der Schnittstellen) wird die rote Strecke um ein Symbol weiter gedreht und die blaue Strecke erneut im Uhrzeigersinn bis zu 16 mal verschoben. Dies muss gemacht werden, bis sich alle rot - blauen Schnittstellen decken, also grün umrandet sind. (Bei 10 Schnittstellen gibt es nur zwei mögliche zwischen rot und blau) Ist das erreicht, wird die silberen Strecke gedreht, bis sich alle Schnittstellen decken. Sollte es keine komplette Lösung geben, obwohl die Schnittstellen der blau - roten Strecken richtig waren, muss nach einer anderen Kombination zwischen blau und rot gesucht werden, um danach wieder die silberne Strecke zu bewegen. Die Reihenfolge der Verschiebung der Strecken ist auch hier unbedeutend, wobei es sich empfiehlt erst die Strecken mit den geringsten Schnittpunkten zu wählen. Geübte Rätsellöser werden durch genaue Betrachtung des Bildes schon vorher einige Möglichkeiten ausschließen können und sich durch Kombinationsgabe schneller zum Ziel bewegen. Allen anderen bleibt erstmal nur der Weg des mühsamen Verschiebens der Strecken, was aber auch zur Lösung verhelfen wird. Viel Erfolg und schöne Belohnungen. | |