Keltischer Knoten: Unterschied zwischen den Versionen
Aus SchnuppTrupp
Anna (Diskussion | Beiträge) |
Anna (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
{{baustelle}} | {{baustelle}} | ||
| + | <br> | ||
| + | {| cellspacing="1" cellpadding="1" border="1" style="width: 771px; height: 1205px;" | ||
| + | |- | ||
| + | | | ||
| + | Das Grundprinzip dieses Rätsels besteht darin, daß unterschiedliche Symbole auf Strecken wahllos angeordnet sind. | ||
| + | |||
| + | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch farbige Punkte)</span> | ||
| + | |||
| + | Ein oder mehrere Symbole sind auf allen Strecken gleich, wenn auch nicht auf gleicher Position. | ||
| + | |||
| + | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch Punkte mit einem X)</span> | ||
| + | |||
| + | An den Stellen, an denen sich die Strecken überschneiden, entstehen Schnittpunkte. | ||
| + | |||
| + | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand)</span> | ||
| + | |||
| + | Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen. | ||
| − | + | | [[Image:Keltischer-knoten-grundprinzip.jpg|500px]] | |
| − | + | ||
| − | + | ||
| − | | [[Image:Keltischer-knoten-grundprinzip.jpg| | + | |
|- | |- | ||
| | | | ||
| Zeile 18: | Zeile 32: | ||
|} | |} | ||
| − | + | <br> | |
{| cellspacing="1" cellpadding="1" border="1" style="width: 452px; height: 700px;" | {| cellspacing="1" cellpadding="1" border="1" style="width: 452px; height: 700px;" | ||
Version vom 20. Oktober 2010, 14:55 Uhr
| Abbildung | |
|---|---|

| |
| 6-übereinstimmenden Feldern | 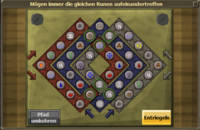
|
| 8-übereinstimmenden Feldern | 
|
| 10-übereinstimmenden Feldern | 
|
| 12-übereinstimmenden Feldern | 
|


