Keltischer Knoten: Unterschied zwischen den Versionen
Anna (Diskussion | Beiträge) |
Anna (Diskussion | Beiträge) |
||
| Zeile 8: | Zeile 8: | ||
Das Grundprinzip dieses Rätsels besteht darin, daß unterschiedliche Symbole auf Strecken wahllos angeordnet sind. | Das Grundprinzip dieses Rätsels besteht darin, daß unterschiedliche Symbole auf Strecken wahllos angeordnet sind. | ||
| − | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch farbige Punkte | + | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch farbige Punkte)</span> |
Ein oder mehrere Symbole sind jedoch auf allen Strecken gleich, wenn auch nicht auf gleicher Position. | Ein oder mehrere Symbole sind jedoch auf allen Strecken gleich, wenn auch nicht auf gleicher Position. | ||
| Zeile 14: | Zeile 14: | ||
<span style="font-size: smaller;">(In der Grafik gekennzeichnet durch Punkte mit einem <span style="background-color: rgb(204, 255, 255);">'''X'''</span>)</span> | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch Punkte mit einem <span style="background-color: rgb(204, 255, 255);">'''X'''</span>)</span> | ||
| − | An den Stellen, an denen sich die Strecken überschneiden, entstehen Schnittpunkte. | + | An den Stellen, an denen sich die Strecken überschneiden, entstehen Schnittpunkte. |
<span style="font-size: smaller;">(In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand <span style="color: rgb(255, 0, 0);">O</span>)</span> | <span style="font-size: smaller;">(In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand <span style="color: rgb(255, 0, 0);">O</span>)</span> | ||
| Zeile 20: | Zeile 20: | ||
Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen. | Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen. | ||
| − | <span style="color: rgb(255, 255, 255);">xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx</span><br> | + | <span style="color: rgb(255, 255, 255);">xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx</span><br> |
| [[Image:Keltischer-knoten-grundprinzip.jpg|500px]] | | [[Image:Keltischer-knoten-grundprinzip.jpg|500px]] | ||
| Zeile 35: | Zeile 35: | ||
<span style="font-size: smaller;">(Vorweginformation für die späteren RS Keltische Knoten: Der rote Rand der Schnittstelle bleibt vorerst rot, da sich noch keine zwei gleichen Symbole getroffen haben. Erst wenn die übereinanderliegenden Symbole identisch sind, wird die rote Umrandung in grün angezeigt - für richtig)</span> | <span style="font-size: smaller;">(Vorweginformation für die späteren RS Keltische Knoten: Der rote Rand der Schnittstelle bleibt vorerst rot, da sich noch keine zwei gleichen Symbole getroffen haben. Erst wenn die übereinanderliegenden Symbole identisch sind, wird die rote Umrandung in grün angezeigt - für richtig)</span> | ||
| − | Jetzt muß die blaue Strecke bewegt werden, um das mit '''<span style="background-color: rgb(204, 255, 255);">X</span>''' gekennzeichnete Symbol ebenfalls zum Schnittpunkt <span style="color: rgb(255, 0, 0);">O </span>zu bewegen. Drei-maliges Verschieben der blauen Strecke in Pfeilrichtung bringt uns zur Lösung.<span style="font-size: smaller;">(Schritt 2)</span><br> | + | Jetzt muß die blaue Strecke bewegt werden, um das mit '''<span style="background-color: rgb(204, 255, 255);">X</span>''' gekennzeichnete Symbol ebenfalls zum Schnittpunkt <span style="color: rgb(255, 0, 0);">O </span>zu bewegen. Drei-maliges Verschieben der blauen Strecke in Pfeilrichtung bringt uns zur Lösung.<span style="font-size: smaller;">(Schritt 2)</span><br> |
<span style="font-size: smaller;">(Vorweginformation für die späteren RS Keltische Knoten: Jetzt ändert sich die Farbe des Randes der Schnittstelle in grün, um uns anzuzeigen, daß wir 2 gleiche Symbole übereinanderliegen haben)</span> | <span style="font-size: smaller;">(Vorweginformation für die späteren RS Keltische Knoten: Jetzt ändert sich die Farbe des Randes der Schnittstelle in grün, um uns anzuzeigen, daß wir 2 gleiche Symbole übereinanderliegen haben)</span> | ||
| Zeile 43: | Zeile 43: | ||
| [[Image:Keltischer-knoten-einführung.jpg|450px]] | | [[Image:Keltischer-knoten-einführung.jpg|450px]] | ||
|- | |- | ||
| − | | <br> | + | | <br> |
| [[Image:Keltischer-knoten-einführung1.jpg|450px]] | | [[Image:Keltischer-knoten-einführung1.jpg|450px]] | ||
|- | |- | ||
| − | | <br> | + | | <br> |
| <br> | | <br> | ||
|} | |} | ||
| Zeile 54: | Zeile 54: | ||
{| cellspacing="1" cellpadding="1" border="1" style="width: 452px; height: 700px;" | {| cellspacing="1" cellpadding="1" border="1" style="width: 452px; height: 700px;" | ||
|- | |- | ||
| − | ! <br> | + | ! <br> |
! Abbildung | ! Abbildung | ||
|- | |- | ||
| − | | <br> | + | | <br> |
| align="center" | [[Image:Keltischer-knoten.png|200px]] | | align="center" | [[Image:Keltischer-knoten.png|200px]] | ||
|- | |- | ||
Version vom 20. Oktober 2010, 15:47 Uhr
Diese Seite befindet sich noch im Aufbau
|
Das Grundprinzip dieses Rätsels besteht darin, daß unterschiedliche Symbole auf Strecken wahllos angeordnet sind. (In der Grafik gekennzeichnet durch farbige Punkte) Ein oder mehrere Symbole sind jedoch auf allen Strecken gleich, wenn auch nicht auf gleicher Position. (In der Grafik gekennzeichnet durch Punkte mit einem X) An den Stellen, an denen sich die Strecken überschneiden, entstehen Schnittpunkte. (In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand O) Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen. xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx |
|
|
Beispiel: Wir haben eine rote und eine blaue Strecke, auf der unterschiedliche Symbole angeordnet sind. Wobei es im Beispiel unerheblich ist, welche Symbole sich hinter den lila oder gelben Punkten verbergen. Konzentrieren wir uns auf die Symbole, die mit einem X gekennzeichnet sind und die sowohl auf der roten als auf der blauen Linie (Strecke) zu finden sind. Stellen wir uns diese Strecken nun als Fließbänder vor, die bewegt werden können. Um das X gekenntzeichnete Symbol auf der roten Strecke zum Schnittpunkt O der beiden Strecken zu bringen, muß die rote Strecke einmal nach rechts verschoben werden. (Schritt 1) (Vorweginformation für die späteren RS Keltische Knoten: Der rote Rand der Schnittstelle bleibt vorerst rot, da sich noch keine zwei gleichen Symbole getroffen haben. Erst wenn die übereinanderliegenden Symbole identisch sind, wird die rote Umrandung in grün angezeigt - für richtig) Jetzt muß die blaue Strecke bewegt werden, um das mit X gekennzeichnete Symbol ebenfalls zum Schnittpunkt O zu bewegen. Drei-maliges Verschieben der blauen Strecke in Pfeilrichtung bringt uns zur Lösung.(Schritt 2) (Vorweginformation für die späteren RS Keltische Knoten: Jetzt ändert sich die Farbe des Randes der Schnittstelle in grün, um uns anzuzeigen, daß wir 2 gleiche Symbole übereinanderliegen haben)
|
|
| |
|
| |
|
| |
Abbildung |
|---|---|
| |
|
| 6-übereinstimmenden Feldern |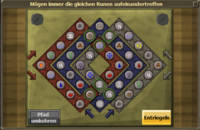 
|
| 8-übereinstimmenden Feldern | 
|
| 10-übereinstimmenden Feldern | 
|
| 12-übereinstimmenden Feldern | 
|
