Keltischer Knoten

Diese Seite befindet sich noch im Aufbau

Das Grundprinzip dieses Rätsels besteht darin, daß unterschiedliche Symbole auf Strecken wahllos angeordnet sind. (In der Grafik gekennzeichnet durch farbige Punkte) Ein oder mehrere Symbole sind jedoch auf allen Strecken gleich, wenn auch nicht auf gleicher Position. (In der Grafik gekennzeichnet durch Punkte mit einem X) An den Stellen, an denen sich die Strecken überschneiden, entstehen Schnittpunkte. (In der Grafik gekennzeichnet durch einen Kreis mit rotem Rand  O) Ziel ist es: Durch Verschieben der Strecken gleiche Symbole auf die Schnittpunkte zu bringen, sodaß sie übereinander liegen. xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Beispiel: Wir haben eine rote und eine blaue Strecke, auf der unterschiedliche Symbole angeordnet sind. Wobei es im Beispiel unerheblich ist, welche Symbole sich hinter den lila oder gelben Punkten verbergen. Konzentrieren wir uns auf die Symbole, die mit einem X gekennzeichnet sind und sich sowohl auf der roten als auf der blauen Linie (Strecke) befinden. Stellen wir uns diese Strecken nun als Fließbänder vor, die bewegt werden können. (Schritt 1) Um das X gekenntzeichnete Symbol auf der roten Strecke zum Schnittpunkt O der beiden Strecken zu bringen, muß die rote Strecke einmal nach rechts verschoben werden. (Vorweginformation für die späteren RS Keltische Knoten: Der rote Rand der Schnittstelle bleibt vorerst rot, da sich noch keine zwei gleichen Symbole getroffen haben. Erst wenn die übereinanderliegenden Symbole identisch sind, wird die rote Umrandung in grün angezeigt - für richtig) (Schritt 2) Jetzt muß die blaue Strecke bewegt werden, um das mit X gekennzeichnete Symbol ebenfalls zum Schnittpunkt O zu bewegen. Drei-maliges Verschieben der blauen Strecke in Pfeilrichtung bringt uns zur Lösung. (Vorweginformation für die späteren RS Keltische Knoten: Jetzt ändert sich die Farbe des Randes der Schnittstelle in grün, um uns anzuzeigen, daß wir 2 gleiche Symbole übereinanderliegen haben) Die Reihenfolge, in der die Strecken verschoben werden, ist unerheblich. Man hätte im Beispiel auch zuerst mit der blauen Strecke beginnen können.
In diesem Beispiel haben wir 3 Strecken mit unterschiedlichen Symbolen und Schnittpunkten. Am Schnittpunkt silber - blau können sich die X , am Schnittpunkt silber - rot die Y und am Schnittpunkt blau - rot die mit Z gekennzeichneten Symbole treffen. (Schritt 1) Beginnen wir mit der grauen Strecke und verschieben sie um zwei Positionen in Pfeilrichtung. Sowohl das X als auch das Y befinden sich jetzt an Schnittpunkten. Da sie sich noch nicht mit den anderen Symbolen auf den Schnittpunkten decken, bleiben sie weiterhin rot-umrandet. (Diese Information ist für die späteren Rs Keltische Knoten von Bedeutung) (Schritt 2) Bewegen wir jetzt die rote Strecke um eine Postition in Pfeilrichtung, erkennen wir, daß die Y Symbole auf der Schnittstelle silber- rot übereinstimmen und somit die Schnittstelle grün-umrandet wird. Das Z Symbol der roten Strecke ist zwar schon auf der richtigen Position der Schnittstelle blau - rot, aber deckt sich noch nicht mit dem Z Symbol der blauen Strecke und bleibt daher rot- umrandet. (Schritt 3) Jetzt bewegen wir die blaue Strecke um 3 Positionen in Pfeilrichtung und erhalten sowohl auf der silber - blauen als auch auf der blau - roten Schnittstelle Übereinstimmungen mit den bereits dahinverschobenen Symbolen X und Z der anderen Strecken. Die Umrandung der Schnittstellenfelder wird nun grün angezeigt, was die Richtigkeit bestätigt.

	Abbildung
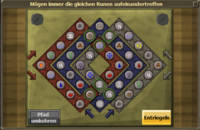
6-übereinstimmenden Feldern
8-übereinstimmenden Feldern
10-übereinstimmenden Feldern
12-übereinstimmenden Feldern